A Novel High-Order Surface Characteristics Scheme for the Neutron Transport Equation in 2D Unstructured Meshes

The development of higher-order method of characteristics (MOC) discretizations has become of great interest to improve the performance of solvers based on the standard Stepwise Constant (SC) MOC approximation. Many codes nowadays implement a Stepwise Linear (SL) volume flux approximation or diamond differencing schemes. In the multigroup lattice solver TDT of the industrial code APOLLO3®, developed at CEA, a Linear Surface (LS) scheme was implemented. In this method, the flux is reconstructed from a linear interpolation made from surface values, therefore ensuring a similar spatial linear development but with a lower computational cost than the volume-based approximations. However, the LS-MOC scheme can conserve only the constant spatial moment of the flux. To overcome this limitation, in this paper we propose an improved version of the LS scheme called LS-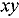 able to preserve the linear spatial moments of the flux. Compared to the other high-order volume-based approximations, the LS- 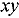scheme also preserves flux surface moments, which guarantees higher accuracy. Moreover, our scheme has a lower memory footprint because it does not require the storage of response matrices that are dependent on region, group, and anisotropy order. Tests carried out on severe rodded assembly cases show the superior performance of the proposed method with respect to not only the classic SC or LS MOC scheme but also the SL scheme.