High-Order Perturbation Method for Updating Response Functions for Time-Dependent Transport Calculations

The hybrid stochastic deterministic continuous-energy coarse mesh transport method (COMET) has been recently extended for high-fidelity efficient kinetics calculations in highly heterogeneous reactor cores. The method discretizes the time variable as a series of time grids and solves the resulting set of steady-state neutron transport equations. In this work, a high-order perturbation method is developed to update the COMET unperturbed response function library on the fly for changes in the discretized time step size 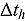. The unperturbed response functions are precomputed with . The perturbation expansion coefficients are also generated during the unperturbed response function library precomputation. The adjoint solution needed by the perturbation method is calculated using the reciprocity relation without solving the corresponding adjoint problems. As a result, the method can be easily implemented into any stochastic code to generate the perturbation expansion coefficients together with the unperturbed response functions.

The high-order perturbation method is benchmarked by comparing both the response functions and the time-dependent COMET core solution (fission density) with the corresponding reference solutions. It is found that the response functions generated by the perturbation method at second order are in excellent agreement with those directly computed by the Monte Carlo method. When 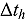changes from 1.0E-4 s to infinity, the average and maximum relative differences in the various response functions were found to be in the range of 0.0000106% to 0.00116% and 0.000011% to 0.00121%, respectively. The fission density as a function of time calculated by COMET using the perturbation method is in excellent agreement with the reference solutions, with an average relative difference of 0.0065% to 0.075%. These comparisons indicate that the perturbation method at second order is highly accurate.