A Quasi–Monte Carlo Method With Krylov Linear Solvers for Multigroup Neutron Transport Simulations

In this work we investigate replacing standard quadrature techniques used in deterministic linear solvers with a fixed-seed Quasi–Monte Carlo (QMC) calculation to obtain more accurate and efficient solutions to the neutron transport equation (NTE). QMC is the use of low-discrepancy sequences to sample the phase-space in place of pseudorandom number generators used by traditional Monte Carlo (MC). QMC techniques decrease the variance in the stochastic transport sweep and therefore increase the accuracy of the iterative method. Historically, QMC has largely been ignored by the particle transport community because it breaks the Markovian assumption needed to model scattering in analog MC particle simulations. However, by using iterative methods the NTE can be modeled as a pure-absorption problem. This removes the need to explicitly model particle scattering and provides an application well suited for QMC. To obtain solutions we experimented with three separate iterative solvers: the standard Source Iteration (SI) Solver and two linear Krylov Solvers, i.e., the Generalized Minimal RESidual method (GMRES) and the BiConjugate Gradient STABilized method (BiCGSTAB). The resulting hybrid iterative-QMC solver was assessed on three slab geometry problems of one dimension. In each sample problem the Krylov Solvers achieve convergence with far fewer iterations (up to eight times) than the SI Solver. Regardless of the linear solver used, the hybrid method achieved an approximate convergence rate of 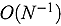as compared to the expected 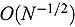of traditional MC simulation across all test problems.