Infiltration and Evaporation in Multiplying Porous Media and Associated Criticality Phenomena

We describe the manner and rate at which water infiltrates and/or transpires into a drum of dry uranium dioxide powder. The powder is 5% enriched and so the possibility of a critical state is possible. In view of the porous nature of the powder, it will exhibit all the characteristics of soil and hence the motion of the water will be described by the use of the methods developed over many years in the field of soil science. The basic phenomena of flow in porous media are described by Richards’ equation, which leads to the moisture concentration 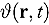from which we may obtain the local density of water. This, together with the fissile cross section of the powder, will enable us to calculate the multiplication rate of the neutron population. The neutron source term arises naturally from spontaneous fission and various 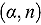reactions. Several scenarios are described, but the two most important cases are (1) when water enters the drum from the top and infiltrates downward, and (2) when water leaks in from the base and capillary forces draw the water upward. Both situations can occur simultaneously depending on the damage sustained by the drum. By damage we do not necessarily mean mechanical due to impact, but also by corrosion if the drum is left unattended in a damp environment. With the space and time dependence of the water concentration available, we can solve the corresponding transport or diffusion equations for the neutron flux and hence calculate the energy produced. In this introductory paper, we do not include feedback, and so in principle, when the water reaches the boiling point our calculations must cease. However, the crucial point is whether criticality will occur, and this can be decided by the value of the multiplication factor 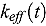. We use the Broadbridge and White model for the porous medium and consider the influence of the porous structure on the value of 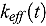. A range of examples is considered both with infiltration and transpiration, and it is shown that the likelihood of criticality is high although less likely for transpiration.