Transport Calculation of the Multiplicity Moments for Cylinders

In a previous paper by Pázsit and Pál [“Multiplicity Theory Beyond the Point Model,” Ann. Nucl. Energy, Vol. 154 (2021)], a general transport theory calculation of the factorial moments of the number of neutrons emitted spontaneously from a sample was elaborated. In contrast to the original derivations by Hage and Cifarelli [“On the Factorial Moments of the Neutron Multiplicity Distribution of Fission Cascades,” Nucl. Instrum. Meth. Phys. Res. A, Vol. 236 (1985)] and Böhnel [“The Effect of Multiplication on the Quantitative Determination of Spontaneously Fissioning Isotopes by Neutron Correlation Analysis,” Nucl. Sci. Eng., Vol. 90 (1985)], also referred to as the point model, in the transport model the spatial and angular dependence of the internal fission chain is taken into account with a one-speed transport theory treatment. Quantitative results were given for a spherical item, and the bias of the point model regarding the estimation of the fission rate as compared to the more exact space-dependent model was estimated as a function of the size of the sphere and the 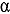factor.

In the present paper the formalism and the quantitative work are extended to the treatment of items with cylindrical shapes, which are more relevant in many practical applications. Results are presented for both square cylinders (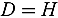) and for tall (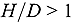) and flat (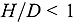) cylinders. This way the differences between the cylinder and the sphere on one hand and those between the various cylinder shapes on the other hand can be estimated. The results show that the bias depends on the geometry of the cylinder quite moderately, but similarly to the case of the sphere, the bias of the point model is quite significant for larger item sizes and 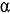values, and it is nonconservative (underestimates the fissile mass) as well.