The Finite-Element with Discontiguous-Support Method

Energy discretization of the transport equation is difficult due to numerous strong, narrow cross-section (XS) resonances. The standard traditional multigroup (MG) method can be sensitive to approximations in the weighting spectrum chosen for XS averaging, which can lead to inaccurate treatment of important phenomena such as self-shielding. We generalize the concept of a group to a discontiguous range of energies to create the Finite-Element with Discontiguous-Support (FEDS) method. FEDS uses clustering algorithms from machine learning to determine optimal definitions of discontiguous groups. By combining parts of multiple resonances into the same group, FEDS can accurately treat resonance behavior even when the number of groups is orders of magnitude smaller than the number of resonances. In this paper, we introduce the theory of the FEDS method and describe the workflow needed to use FEDS, noting that ordinary MG codes can use FEDS XSs without modification, provided these codes can handle upscattering. This allows existing MG codes to produce FEDS solutions. In the context of light water reactors, we investigate properties of FEDS XSs compared to MG XSs and compare 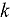-eigenvalue and reaction rate quantities of interest to continuous-energy Monte Carlo, showing that FEDS provides higher accuracy and less cancellation of error than MG with expert-chosen group structures.