A New Proof of the Asymptotic Diffusion Limit of the SN Neutron Transport Equation
Nuclear Science and Engineering / Volume 195 / Number 12 / December 2021 / Pages 1347-1358
Technical Note / dx.doi.org/10.1080/00295639.2021.1924048
Articles are hosted by Taylor and Francis Online.
It has been well known that the analytic neutron transport solution tends to the analytic solution of a diffusion problem for optically thick systems with small absorption and source. The standard technique for proving the asymptotic diffusion limit is constructing an asymptotic power series of the neutron angular flux in small positive parameter 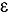 , which is the ratio of a typical mean free path of a particle to a typical dimension of the problem domain. In this paper, first, we provide an analysis of the asymptotic properties of the SN transport eigenvalues. Then, we show that the analytical SN transport solution satisfies the diffusion equation in the asymptotic diffusion limit based on a recently obtained closed-form analytical solution to the one-dimensional monoenergetic SN neutron transport equation. The boundary conditions for the diffusion equation are discussed.
, which is the ratio of a typical mean free path of a particle to a typical dimension of the problem domain. In this paper, first, we provide an analysis of the asymptotic properties of the SN transport eigenvalues. Then, we show that the analytical SN transport solution satisfies the diffusion equation in the asymptotic diffusion limit based on a recently obtained closed-form analytical solution to the one-dimensional monoenergetic SN neutron transport equation. The boundary conditions for the diffusion equation are discussed.


