An Analytic Benchmark for Neutron Boltzmann Transport with Downscattering—Part I: Flux and Eigenvalue Solutions

Computing in the energy dimension is one of the greatest challenges confronting present-day deterministic neutron transport solvers. Accurately resolving the neutron flux as neutrons downscatter across resonances in the nuclear cross sections currently requires considerable computing power and suffers from approximation errors. Flux uncertainty resulting from the uncertainty of the resonance structure is the single-largest cause of reactivity uncertainty. Any additional reference solution for the critical neutron downscattering problem with resonance phenomena would be a boon to verification and validation of neutronics codes.

This paper establishes a benchmark to verify the accuracy of neutron transport criticality solvers along the energy dimension. For the first time, the analytic solution of the flux amplitude is derived in the particular case of an infinite homogeneous medium with isotropic scattering in the center of mass and an arbitrary number of no-threshold, neutral particle reaction resonances (e.g., radiative capture, fission, and resonance scattering). Original analytic expressions are established to quantify the discrepancy between the 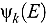and 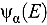flux amplitudes, respective solutions of the multiplication factor 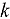, or the exponential time-evolution frequency 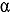eigenproblems. The physical study of these relations led to analysis of their first-order relative difference near the criticality condition 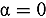. Finally, numerical solutions are provided to a benchmark problem constituted of the first resonance of ²³⁹Pu, the 6.67-eV resonance of ²³⁸U, and a scattering isotope with a flat cross section, allowing for the computational verification of the energy resolution of current neutron transport criticality codes. Through these novel results, this analytic benchmark can serve as a reference to verify the energy resolution and sensitivity analysis of neutron transport criticality calculations.