The Asymptotic Diffusion Limit of Numerical Schemes for the S_N Transport Equation

The S_N transport equation asymptotically tends to an equivalent diffusion equation in the limit of optically thick systems with small absorption and sources. A spatial discretization of the S_N equation is of practical interest if it possesses the optically thick diffusion limit. Such a numerical scheme will yield accurate solutions for diffusive problems if the spatial mesh size is thin with respect to a diffusion length, whereas the mesh cells are thick in terms of a mean free path. Many spatial discretization methods have been developed for the S_N transport equation, but only a few of them can obtain the thick diffusion limit under certain conditions. This paper presents a theoretical result that simply states that the mesh size required for a finite difference scheme to attain the diffusion limit is 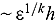, where 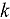is the order of accuracy of spatial discretization, 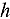is the “diffusion” mesh size that can be many mean free paths thick, and 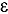is a small positive scaling parameter that can be defined as the ratio of a particle mean free path to a characteristic scale length of the system. Numerical results for schemes such as the Diamond Difference method, Step Characteristic method, Step Difference method, Second-Order Upwind method, and Lax-Friedrichs Weighted Essentially Non-Oscillatory method of the third order (LF-WENO3) are presented that demonstrate the validity and accuracy of our analysis.