Calculating the k-Eigenvalue Sensitivity to Typical Geometric Perturbations with the Adjoint-Weighted Method in the Continuous-Energy Reactor Monte Carlo Code RMC

Geometric sensitivity analyses of the 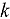-eigenvalue have many applications in analyses of geometric uncertainty, calculations of differential control rod worth, and searches for critical geometry. The adjoint-weighted first-order geometric sensitivity theory is widely used and has continuously evolved with the Monte Carlo methods. However, the existing adjoint-weighted algorithm can do only uniform isotropic expansions or contractions of surfaces. The adjoint-weighted algorithm also requires computation of adjoint-weighted scattering and fission reaction rates exactly at material interfaces, which has an infinitesimal probability in reality. This paper presents an improved geometry adjoint-weighted perturbation algorithm that is incorporated into the continuous-energy Reactor Monte Carlo (RMC) code. The improvement of the adjoint-weighted algorithm is decomposed into three steps for constructing a cross-section function of geometric parameters using logical expressions, calculating the derivative of the cross-section function, and estimating the adjoint-weighted surface reaction rates. The improved algorithm can accommodate common one-parameter geometric perturbations of internal interfaces or boundary surfaces as well as those of cells as long as the perturbed cells can be described by logical expressions of spatial surface equations. The perturbation algorithm is compared with a direct difference method, the linear least-squares fitting method with central differences, for several typical geometric perturbations including translation, fixed-axis rotation, and uniform isotropic/anisotropic expansion transformations of planar, spherical, cylindrical, and conical surfaces. The differences between the two methods are not more than 3% and not more than 3 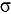for the majority of the test examples. Even though the perturbation algorithm has higher figures of merit than the direct difference method for the majority of the test examples, there is no guarantee that the former can always be more efficient than the latter. The limitation in the efficiency of the perturbation algorithm was demonstrated by the totally reflecting light water reactor pin model.