The Screened Rutherford Pencil Beam Problem with Heterogeneities

We consider the energy-dependent pencil beam problem for a thin slab with screened Rutherford scattering. Under certain approximations, this problem can be reduced to a monoenergetic problem with an effective depth-dependent scattering cross section [overbar]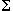_s(z). The z dependence of this cross section arises from the explicit z dependence of the true scattering cross section 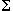_s(z,E), as well as from an induced z dependence associated with the energy dependence of 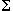_s(z,E). Prior work led to a quadrature result for the scalar flux in the special case that [overbar]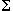_s is a constant, independent of z. In this paper, we generalize this result by allowing [overbar]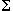_s(z) to have an arbitrary z dependence. We use these considerations to show that simple homogenization, namely, replacing [overbar]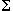_s(z) by its average over the slab, can lead to significant errors in the scalar flux. A more detailed homogenization algorithm is suggested, involving an effective screening parameter in the screened Rutherford scattering phase function, as well as an effective depth coordinate z.