Thermal-Neutron Space-Time Decay Constants in Various Order PN Approximations
Nuclear Science and Engineering / Volume 20 / Number 4 / December 1964 / Pages 414-427
Technical Paper / dx.doi.org/10.13182/NSE64-A20983
Articles are hosted by Taylor and Francis Online.
The thermal neutron space-time eigenvalue spectrum of the multigroup PN approximation is investigated numerically for a modified form of the Radkowsky Kernel. Both discrete eigenvalues and eigenvalues that are assigned to a ‘continuum region,’ on the grounds that the corresponding eigenvectors exhibit singularities, are found. The continuum region so defined agrees well with that expected for the Boltzmann Equation. It is found that, when λ, the time decay constant, is plotted vs B2, the square of the geometrical buckling, there is in the PN approximation a critical value 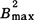 beyond which no real eigenvalues λ exist. The value of
beyond which no real eigenvalues λ exist. The value of 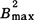 is sensitive to the order of the PN approximation, increasing with increasing N. It is conjectured that
is sensitive to the order of the PN approximation, increasing with increasing N. It is conjectured that 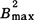 corresponds, when the extrapolated endpoint is considered, to a slab of zero thickness through which a burst of neutrons would pass undisturbed as an ideal travelling wave.
corresponds, when the extrapolated endpoint is considered, to a slab of zero thickness through which a burst of neutrons would pass undisturbed as an ideal travelling wave.


