The Stochastic Behavior of the Eigenvalue Due to Spatial Perturbation in the Fuel Distribution of the One-Speed Slab Reactor
Nuclear Science and Engineering / Volume 130 / Number 1 / September 1998 / Pages 85-97
Technical Paper / dx.doi.org/10.13182/NSE98-A1992
Articles are hosted by Taylor and Francis Online.
The behavior of the average eigenvalue <keff> of the critical one-speed slab reactor is analyzed as a function of local density fluctuation, while keeping the total material loading of the reactor constant, using a combination of analytical and numerical methods. A perturbation of the reference reactor as a binary material medium is used as developed by Pomraning. Two parallel probability distributions are utilized, and the averages as obtained in the corresponding ensembles are compared. These two distributions provide a heuristic description of the physical effects of the spatial perturbation and a methodology that can be extended to practical problems. The sources of increase and decrease in the eigenvalues of the perturbed configurations are identified, and their relative strengths are identified as functions of the reemission factor c. The average eigenvalue is found to always increase for the perturbations and distributions considered and is plotted as function of c from c = 1 to . As the number of regions N (even integer) in the binomial distribution is increased, the number of possible perturbed configurations increases rapidly such that the new members of the ensemble are closer to the reference reactor in fuel distribution, and thus each has an eigenvalue keff increasingly closer to 1. Since these new members predominate the ensemble at large N, <keff> tends to 1 strictly from above as N increases. A similar behavior is observed with the exponential distribution but is tied to the average binary material thickness or the exponential distribution correlation length
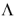 c. The analysis also shows that (using either distribution) for the same c, <keff> is larger for systems with less scattering in the corresponding reference reactor. In other words, for a fixed c, the maximum <keff> is when
c. The analysis also shows that (using either distribution) for the same c, <keff> is larger for systems with less scattering in the corresponding reference reactor. In other words, for a fixed c, the maximum <keff> is when 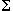 s = 0, and the minimum is when
s = 0, and the minimum is when 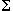 a = 0 in the corresponding reference reactors. Some of the conditions on the stochastic perturbation distribution and the cross-section components that are necessary (but may not be sufficient) to produce <keff> below 1 are identified.
a = 0 in the corresponding reference reactors. Some of the conditions on the stochastic perturbation distribution and the cross-section components that are necessary (but may not be sufficient) to produce <keff> below 1 are identified.


